Funciones Trigonométricas


Facultad de Matemáticas UC
Nota.
Todas las fórmulas que serán presentadas en esta clase son válidas tanto para
ángulos en grados como para ángulos en radianes.
Fórmulas de par-impar
1. \(\sin\left(-t\right)=-\sin(t)\)
2. \(\cos\left(-t\right)=\cos(t)\)
3. \(\tan\left(-t\right)=-\tan(t)\)
Fórmulas de Cofunción
1. \(\sin\left(\dfrac{\pi}{2}-t\right)=\cos(t)\)
2. \(\cos\left(\dfrac{\pi}{2}-t\right)=\sin(t)\)
3. \(\tan\left(\dfrac{\pi}{2}-t\right)=\cot(t)\)
Ejemplo.
Sea \(t\) un ángulo en el tercer cuadrante tal que \(\cos(t)=-\dfrac{3}{5}\).
Calcule el valor de \(\cos\left(\dfrac{\pi}{2}+t\right)\).
Fórmulas para suma y diferencia de ángulo
- \(\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\sin(\beta)\cos(\alpha)\)
- \(\sin(\alpha-\beta)=\sin(\alpha)\cos(\beta)-\sin(\beta)\cos(\alpha)\)
- \(\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\)
- \(\cos(\alpha-\beta)=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\)
Ejemplo.
- Justifique, sin usar las fórmulas para suma y diferencia de ángulos, por qué \[ \sin\big(15^{\circ}\big)=\cos\big(75^{\circ}\big) \]
- Usando las fórmulas de suma y diferencia de ángulos calcule o bien \(\sin\big(15^{\circ}\big)\) o bien \(\cos\big(75^{\circ}\big)\) (o ambos).
Ejemplo.
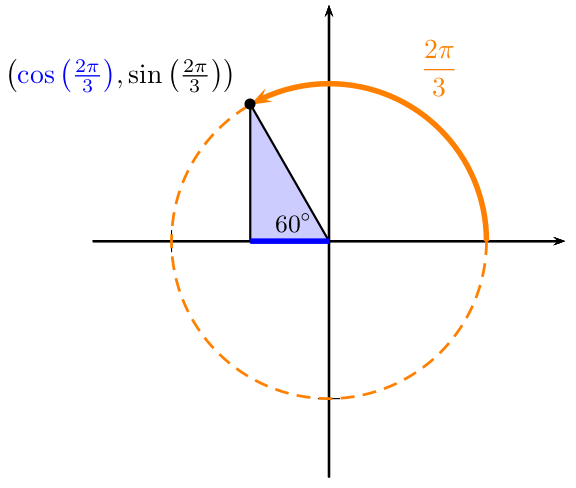
Usando reducción a los ángulos notables se puede probar que
\[
\cos\left(\dfrac{2\pi}{3}\right)=-\cos\big(60^{\circ}\big)=-\dfrac{1}{2}
\]
Pruebe este resultado usando las fórmulas de suma y diferencia
de ángulos para
\[
\cos\left(\dfrac{\pi}{3}+\dfrac{\pi}{3}\right)
\]
Fórmulas para suma y diferencia de ángulo
- \(\tan(\alpha+\beta)=\dfrac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}\)
- \(\tan(\alpha-\beta)=\dfrac{\tan(\alpha)-\tan(\beta)}{1+\tan(\alpha)\tan(\beta)}\)
Ejemplo.
Si \(m=\tan(t)\), demuestre que
\[
\dfrac{\tan\left(\tfrac{\pi}{4}+t\right)}{\tan\left(\tfrac{\pi}{4}-t\right)}=\left(\dfrac{1+m}{1-m}\right)^{2}
\]
Fórmulas para el ángulo doble
- \(\sin(2\alpha)\) \(=2\sin(\alpha)\cos(\alpha)\)
- \(\cos(2\alpha)\) \(=\cos^{2}(\alpha)-\sin^{2}(\alpha)\)
- \(\tan(2\alpha)\) \(=\dfrac{2\tan(\alpha)}{1-\tan^{2}(\alpha)}\)
Ejemplo.
Sea \(\tfrac{\pi}{2} \lt t \lt \pi\) tal que \(\tan(2t)=-\dfrac{5}{12}\).
Determine el valor de \(\tan(t)\).
Tarea.
Si \(\tfrac{\pi}{2} \lt t \lt \pi\) es tal que \(\cos(2t)=-\dfrac{7}{9}\),
calcule \(\tan(t)\).
Sugerencia. Use la fórmula del ángulo doble para el coseno y
la identidad pitagórica \(\cos^{2}(t)+\sin^{2}(t)=1\) para obtener
una ecuación cuadrática en una única función trigonométrica.